Finding Voltage with Ohm's Law
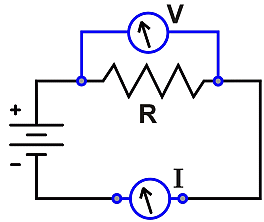
Figure 1. A voltage V dropping across a resistor R in a circuit with a current I. |
In the early 1800's, George Ohm discovered a mathematical relationship for electric circuits with simple resistors. With a circuit having a current I (in amperes), the voltage (V, in volts) dropped across a resistance (R, in ohms) is V = I x R. This relationship often appears three ways:
![]()
![]()
![]()
The first form allows us to calculate the voltage drop across a resistor for a given current in a circuit. Suppose an ammeter measures a current of I = 1.8 amperes through a resistance of R = 3.5 ohm. Then the voltage dropped by the resistance is:
![]()
Notice the units. Remember: The ohm is a unit of resistance, defined as the resistance such that one volt across it will produce one ampere of current through it.
You must be careful working with the units. Currents are often measured in milliamps (1/1,000 ampere) or even microamps (1/1,000,000 ampere). Resistance may be in kilohms (1,000 ohms) or even megohms (1,000,000 ohms).
Suppose a current of 3.9 milliamps passes through a 2.5 megohm resistor. The voltage across the resistor:
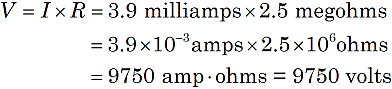
It is often helpful to convert metric prefixes to scientific notation.
|
micro- = 10–6 |
milli- = 10–3 |
kilo- = 103 |
mega- = 106 |
