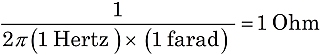Print this

Calculating Reactance

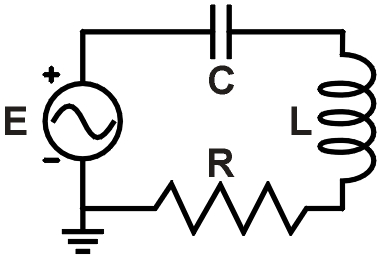f = 4.4 kHz    R = 220 Ω L = 3.6 mH    C = 0.48 μf

Figure 1. Example RLC circuit

The current in a circuit can be "impeded" by three types of circuit components:

• Resistors: contribute resistance, R (in ohms)

• Inductors: contribute inductive reactance, X_L (in ohms)

• Capacitors: contribute capacitive reactance, X_C (in ohms)

Here are the formulas to calculate the last two above, X_L and X_C. Notice that both depend on the AC frequency, f:

   and   

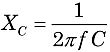
where f is the frequency in Hertz (or sec⁻¹), L is inductance in Henries, and C is capacitance in farads. You will seldom encounter an inductance as large as 1 Henry or a capacitance of 1 farad, but instead deal with prefixes like milli-, micro-, and even pico-.

Inductive reactance

For example, consider the circuit shown in Figure 1. Let's use the formula for X_L to calculate the reactance of the inductor. Converting the prefixes to scientific notation can help avoid mistakes. Note that f = 4.4 kHz = 4.4 x 10³ Hz and L = 3.6 mH = 3.6 x 10⁻³ H.

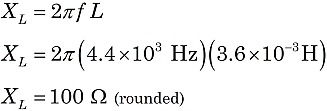
You might notice that the product of kilo- (or 10³) and milli- (or 10⁻³) yields: 10³⋅10⁻³ = 1. That makes the calculation easier: X_L = 2π ⋅ 4.4 ⋅ 3.6 = 100 Ω (rounded).

Capacitive reactance

Similarly, we can use the formula for X_C to calculate the reactance of the capacitor. Again, converting to scientific notation, f = 4.4  x  10³ Hz and C = 0.48 μf = 4.8 x 10⁻⁷ f.

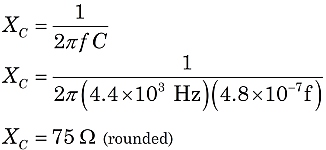
Again, if you are careful with the prefixes, you notice that the product of kilo- (or 10³) and micro- (or 10⁻⁶) yields 10³⋅10⁻⁶ = 10⁻³, or 1/1000. Then X_C = 1000/(2π ⋅ 4.4 ⋅ 0.48) = 75 Ω (rounded).

These electrical units are defined so their products and quotients work out to ohms:

   and